CSP做题记录

发表于 | 分类于 ， | 阅读数

前言

因为老师说CSP过了可以免考数据结构,这么好,当然得报啊。然而,刚碰到第一题就让我想起了高中被算法支配的恐惧了。难道后端检查答案不是直接对比输出的字符串吗？难道还验证输出的数据类型？？？
郁闷至极，这也是我放弃算法比赛的原因之一，脱离实际，考核数据极端，特写此博客让大家避坑。

WP

小中大

一条很简单的签到题，然而就是把我卡在了85，题目如下
test
其中有一个要求及其苛刻,中位数若是整数就输出整数,否则保留一位小数.
第一反应,这还不简单,cout默认就是这样,提交,卡住了.
然后想到了printf中的%g操作符(g格式符，用来输出实数，输出格式为f格式或e格式，系统根据数据占宽度m大小，自动选择占宽度较小的某种格式输出，g格式符不输出小数点后无意义的零。),同样,挂了.
心态大崩,上网搜索题解,无奈,分情况讨论.
以下是源码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
#include <iomanip>
using namespace std;
int n,a[100000+2];
int main()
{
	int max=0x80000000;
	int min=0x7fffffff;

	cin>>n;
	for(int i=0;i<n;i++)
	{
		cin>>a[i];
		if(a[i]<min) min=a[i];
		if(a[i]>max) max=a[i];
	}
	float zhong;
	if(n & 1) //如果n为奇数，中位数不必计算
	{
		printf("%d %d %d", max, a[(n - 1) / 2], min);
	}
	else //如果n为偶数，中位数需要另外计算
	{
		int x1 = a[n / 2 - 1], x2 = a[n / 2];
		if((x1 ^ x2) & 1) //如果参与计算的两个参数奇偶性互异
		{
			double mid = (x1 + x2) / 2.;
			printf("%d %.1lf %d", max, mid, min);
		}
		else //如果参与计算的两个参数奇偶性相同
		{
			printf("%d %d %d", max, (x1 + x2) >> 1, min);
		}
	}
 return 0;
}

85分继续吐槽:一开始猜测是linux和Windows的系统区别导致分数问题，结果？？？真的能识别数据类型？官方没公开测试数据，我也没得办法了。emmm

二十四点

test
初看就是字符串计算问题，一下子想到的是python的eval，啊啊啊啊，python真好，QAQ。这就得让我们自己写栈模拟计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <bits/stdc++.h>
using namespace std;
int n;
string str;
int main()
{
	cin>>n;
	queue<int> num;
	queue<char> op;
	for(int i=0;i<n;i++)
	{
		cin>>str;
		str.push_back('+'); //是末尾为符号位 
		for(int j=1;j<str.length();j+=2)
		{
			int t=(str[j-1]-'0');
			for(;j<str.length()&&(str[j]=='x'||str[j]=='/');j+=2)
			{
				if(str[j]=='x')
					t=t*(str[j+1]-'0');
				else
					t=t/(str[j+1]-'0');	
			}
			num.push(t);
			op.push(str[j]);
		}
		num.push(0);
		int t = num.front();
		num.pop();
		while(!op.empty())
		{
			char c=op.front();
			op.pop();
			if(c=='+')
				t = t + num.front();
			else
				t = t - num.front();
			num.pop();
		}
		if(t==24) cout<<"Yes"<<endl;
		else cout<<"No"<<endl;
	}
	return 0;
}

小明上学

题目背景

　　小明是汉东省政法大学附属中学的一名学生，他每天都要骑自行车往返于家和学校。为了能尽可能充足地睡眠，他希望能够预计自己上学所需要的时间。他上学需要经过数段道路，相邻两段道路之间设有至多一盏红绿灯。
　　京州市的红绿灯是这样工作的：每盏红绿灯有红、黄、绿三盏灯和一个能够显示倒计时的显示牌。假设红绿灯被设定为红灯 r 秒，黄灯 y 秒，绿灯 g 秒，那么从 0 时刻起，[0,r) 秒内亮红灯，车辆不许通过；[r, r+g) 秒内亮绿灯，车辆允许通过；[r+g, r+g+y) 秒内亮黄灯，车辆不许通过，然后依次循环。倒计时的显示牌上显示的数字 l（l > 0）是指距离下一次信号灯变化的秒数。

问题描述

　　一次上学的路上，小明记录下了经过每段路的时间，和各个红绿灯在小明到达路口时的颜色和倒计时秒数。希望你帮忙计算此次小明上学所用的时间。

输入格式

　　输入的第一行包含空格分隔的三个正整数 r、y、g，表示红绿灯的设置。这三个数均不超过 106。
　　输入的第二行包含一个正整数 n（n ≤ 100），表示小明总共经过的道路段数和看到的红绿灯数目。
　　接下来的 n 行，每行包含空格分隔的两个整数 k、t。k=0 表示经过了一段道路，耗时 t 秒，此处 t 不超过 106；k=1、2、3 时，分别表示看到了一个红灯、黄灯、绿灯，且倒计时显示牌上显示的数字是 t，此处 t 分别不会超过 r、y、g。

输出格式

　　输出一个数字，表示此次小明上学所用的时间。

样例输入

30 3 30
8
0 10
1 5
0 11
2 2
0 6
0 3
3 10
0 3

样例输出

70

样例说明

　　小明先经过第一段道路，用时 10 秒，然后等待 5 秒的红灯，再经过第二段道路，用时 11 秒，然后等待 2 秒的黄灯和 30 秒的红灯，再经过第三段、第四段道路，分别用时6、3秒，然后通过绿灯，再经过最后一段道路，用时 3 秒。共计 10 + 5 + 11 + 2 + 30 + 6 + 3 + 3=70 秒。
评测用例规模与约定
　　测试点 1, 2 中不存在任何信号灯。
　　测试点 3, 4 中所有的信号灯在被观察时均为绿灯。
　　测试点 5, 6 中所有的信号灯在被观察时均为红灯。
　　测试点 7, 8 中所有的信号灯在被观察时均为黄灯。
　　测试点 9, 10 中将出现各种可能的情况。

模拟

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <bits/stdc++.h>
using namespace std;
int main()
{
	int i,k,t,time=0,r,y,g,n;
	cin>>r>>y>>g>>n;
	for(i=0;i<n;i++)
	{
		cin>>k>>t;
		if(k==0)
			time+=t;
		if(k==1)
			time+=t;
		if(k==2)
			time+=t+r;
	}	
	printf("%d",time);
	return 0;
}

小明放学

题目背景

　　汉东省政法大学附属中学所在的光明区最近实施了名为“智慧光明”的智慧城市项目。具体到交通领域，通过“智慧光明”终端，可以看到光明区所有红绿灯此时此刻的状态。小明的学校也安装了“智慧光明”终端，小明想利用这个终端给出的信息，估算自己放学回到家的时间。
问题描述
　　一次放学的时候，小明已经规划好了自己回家的路线，并且能够预测经过各个路段的时间。同时，小明通过学校里安装的“智慧光明”终端，看到了出发时刻路上经过的所有红绿灯的指示状态。请帮忙计算小明此次回家所需要的时间。

输入格式

　　
输入的第一行包含空格分隔的三个正整数 r、y、g，表示红绿灯的设置。这三个数均不超过 106。
　　输入的第二行包含一个正整数 n，表示小明总共经过的道路段数和路过的红绿灯数目。
　　接下来的 n 行，每行包含空格分隔的两个整数 k、t。k=0 表示经过了一段道路，将会耗时 t 秒，此处 t 不超过 106；k=1、2、3 时，分别表示出发时刻，此处的红绿灯状态是红灯、黄灯、绿灯，且倒计时显示牌上显示的数字是 t，此处 t 分别不会超过 r、y、g。
输出格式
　　输出一个数字，表示此次小明放学回家所用的时间。

样例输入

30 3 30
8
0 10
1 5
0 11
2 2
0 6
0 3
3 10
0 3

样例输出

46

样例说明

　　小明先经过第一段路，用时 10 秒。第一盏红绿灯出发时是红灯，还剩 5 秒；小明到达路口时，这个红绿灯已经变为绿灯，不用等待直接通过。接下来经过第二段路，用时 11 秒。第二盏红绿灯出发时是黄灯，还剩两秒；小明到达路口时，这个红绿灯已经变为红灯，还剩 11 秒。接下来经过第三、第四段路，用时 9 秒。第三盏红绿灯出发时是绿灯，还剩 10 秒；小明到达路口时，这个红绿灯已经变为红灯，还剩两秒。接下来经过最后一段路，用时 3 秒。共计 10+11+11+9+2+3 = 46 秒。

评测用例规模与约定

　　有些测试点具有特殊的性质：
　　 前 2 个测试点中不存在任何信号灯。
　　测试点的输入数据规模： 　　 前 6 个测试点保证 n ≤ 103。
　　* 所有测试点保证 n ≤ 105。

模拟

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <bits/stdc++.h>
using namespace std;
int main()
{
	long long i,k,t,time=0,r,y,g,n;
	long long all;
	cin>>r>>y>>g>>n;
	all=r+y+g;
	for(i=0;i<n;i++)
	{
		cin>>k>>t;
		if(k==0)
		{
			time+=t;
		}
		if(k==1)
		{
			int tmp=(time+r-t)%all;
			if(tmp>=0&&tmp<r)
			{
				time+=r-tmp;
			}
			else if(tmp>=r+g)
			{
				time+=all-tmp+r;
			}
		}
		if(k==2)
		{
			int tmp=(time+all-t)%all;
			if(tmp>=0&&tmp<r)
			{
				time+=r-tmp;
			}
			else if(tmp>=r+g)
			{
				time+=all-tmp+r;
			}
		}
		if(k==3)
		{
			int tmp=(time+r+g-t)%all;
			if(tmp>=0&&tmp<r)
			{
				time+=r-tmp;
			}
			else if(tmp>=r+g)
			{
				time+=all-tmp+r;
			}
		}
	}	
	printf("%lld\n",time);
	return 0;
}

ps: 一定要注意这题的数据规模。算法正确开int只能60分，long long才能AC。

数据中心

test

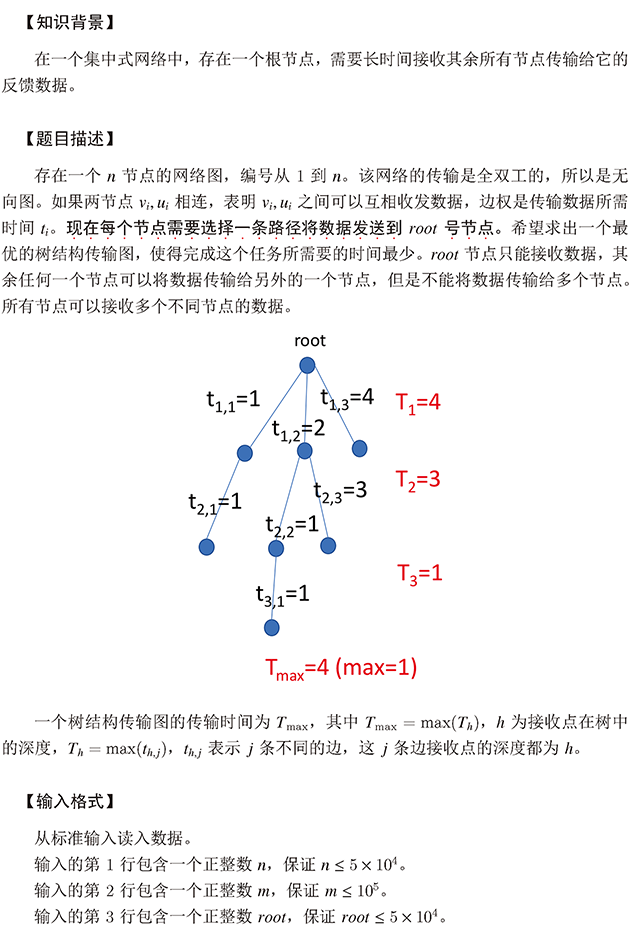
最小生成树算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <bits/stdc++.h>
using namespace std;
struct Edge{
	int start,to;
	int cos;
}edge[500000+2];
int pre[100000+2];
long long ans=0;
int n,m,total=0,u,v,res=0;
int find(int x)
{
	if(pre[x]==x){
		return x;
	}
	else{
		pre[x]=find(pre[x]);
		return pre[x];
	}
}
bool cmp(Edge a,Edge b)
{
	return a.cos<b.cos;
}
inline void kruskal()
{
	for(int i=0;i<m;i++)
	{
		u=find(edge[i].start);
		v=find(edge[i].to);
		if(u==v) continue;
		ans += edge[i].cos;
		res = res>edge[i].cos?res:edge[i].cos;
		pre[u] = v;
		total++;
		if(total == n-1) break;
	}
}
int main()
{
	cin>>n>>m;
	int root;
	cin>>root;
	for(int i=0;i<n;i++) pre[i]=i;
	for(int i=0;i<m;i++)
	{
		cin>>edge[i].start>>edge[i].to>>edge[i].cos;
	}
	sort(edge,edge+m,cmp);
	kruskal();
	cout<<res<<endl;
	return 0;
 }

卖菜

问题描述

　　在一条街上有n个卖菜的商店，按1至n的顺序排成一排，这些商店都卖一种蔬菜。
　　第一天，每个商店都自己定了一个价格。店主们希望自己的菜价和其他商店的一致，第二天，每一家商店都会根据他自己和相邻商店的价格调整自己的价格。具体的，每家商店都会将第二天的菜价设置为自己和相邻商店第一天菜价的平均值（用去尾法取整）。
　　注意，编号为1的商店只有一个相邻的商店2，编号为n的商店只有一个相邻的商店n-1，其他编号为i的商店有两个相邻的商店i-1和i+1。
　　给定第一天各个商店的菜价，请计算第二天每个商店的菜价。

输入格式

　　输入的第一行包含一个整数n，表示商店的数量。
　　第二行包含n个整数，依次表示每个商店第一天的菜价。

输出格式

　　输出一行，包含n个正整数，依次表示每个商店第二天的菜价。

样例输入

8
4 1 3 1 6 5 17 9

样例输出

2 2 1 3 4 9 10 13

数据规模和约定

　　对于所有评测用例，2 ≤ n ≤ 1000，第一天每个商店的菜价为不超过10000的正整数。

水题

1
2
3
4
5
6
7
8
9
10
11
12
13
#include <bits/stdc++.h>
using namespace std;
int n,a[1002];
int main()
{
	cin>>n;
	for(int i=0;i<n;i++) cin>>a[i];
	cout<<(a[0]+a[1])/2<<" ";
	for(int i=1;i<n-1;i++)
		cout<<(a[i-1]+a[i]+a[i+1])/3<<" ";
	cout<<(a[n-1]+a[n-2])/2<<endl;
	return 0;
}

买菜

问题描述

　　小H和小W来到了一条街上，两人分开买菜，他们买菜的过程可以描述为，去店里买一些菜然后去旁边的一个广场把菜装上车，两人都要买n种菜，所以也都要装n次车。具体的，对于小H来说有n个不相交的时间段[a1,b1],[a2,b2]…[an,bn]在装车，对于小W来说有n个不相交的时间段[c1,d1],[c2,d2]…[cn,dn]在装车。其中，一个时间段[s, t]表示的是从时刻s到时刻t这段时间，时长为t-s。
　　由于他们是好朋友，他们都在广场上装车的时候会聊天，他们想知道他们可以聊多长时间。

输入格式

　　输入的第一行包含一个正整数n，表示时间段的数量。
　　接下来n行每行两个数ai，bi，描述小H的各个装车的时间段。
　　接下来n行每行两个数ci，di，描述小W的各个装车的时间段。

输出格式

　　输出一行，一个正整数，表示两人可以聊多长时间。

样例输入

4
1 3
5 6
9 13
14 15
2 4
5 7
10 11
13 14

样例输出

3

数据规模和约定

　　对于所有的评测用例，1 ≤ n ≤ 2000, ai < bi < ai+1，ci < di < ci+1,对于所有的i(1 ≤ i ≤ n)有，1 ≤ ai, bi, ci, di ≤ 1000000。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <bits/stdc++.h>
using namespace std;
int n,ans=0;
struct node{
	int x,y;
}a[2000+2],b[2000+2];
int main()
{
	cin>>n;
	for(int i=0;i<n;i++) cin>>a[i].x>>a[i].y;
	for(int i=0;i<n;i++) cin>>b[i].x>>b[i].y;
	int i=0,j=0;
	while(i<n&&j<n)
	{
		if(a[i].x<=b[j].x)
		{
			if(a[i].y<b[j].x)
			{
				i++;		
			}
			else if(a[i].y>=b[j].y)
			{
				ans+=b[j].y-b[j].x;
				j++;
			}
			else{
				ans+=a[i].y-b[j].x;
				i++;
			}
		}
		else if(a[i].x<b[j].y){
			if(a[i].y<=b[j].y)
			{
				ans+=a[i].y-a[i].x;	
				i++;
			}
			else
			{
				ans+=b[j].y-a[i].x;
				j++;
			}
		}
		else{
			j++;
		}
	}
	cout<<ans<<endl;
	return 0;
}

STL版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<bits/stdc++.h>
using namespace std;
int main(){
    int n,ans=0;//ans存储最终结果
    scanf("%d",&n);
    vector<pair<int,int>>v1(n),v2(n);//分别存储小H和小W的装车时间段
    for(int i=0;i<n;++i)
        scanf("%d%d",&v1[i].first,&v1[i].second);
    for(int i=0;i<n;++i)
        scanf("%d%d",&v2[i].first,&v2[i].second);
    for(pair<int,int>p1:v1)
        for(pair<int,int>p2:v2)
            if(p1.first<=p2.second&&p1.second>=p2.first)//判断有无重叠区间
                ans+=min(p1.second,p2.second)-max(p1.first,p2.first);//加上重叠区间
    printf("%d",ans);
    return 0;
}
//orz,搬运网上的算法显然看起来舒服,不过时间复杂度比我高一些

元素选择器

test

模拟,选好数据结构存储就行。但自己在几个分段卡了很久,这边说一下，供大家避坑。

  1. 大小写问题,开始没仔细读题,id区分大小写,tags不区分
  2. 祖先元素问题,不是它的父节点以及父节点的父节点等等被称作祖先节点,而是比他深度要小的节点都成为其的祖先节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
#include <bits/stdc++.h>
using namespace std;
int n, m;
struct node {
	int fa;
	int level;
	string id;
	string name;
}tags[1002];

vector<int> fa[1002];

int main()
{
	int dotcnt;
	string str;
	cin >> n >> m;
	cin.ignore();
	getline(cin, str);
	tags[0].fa = -1;
	tags[0].name = str;
	tags[0].level = 0;
	fa[0].push_back(0);
	for (int i = 1; i < n; i++)
	{
		getline(cin, str);
		dotcnt=str.rfind('.') + 1;
		tags[i].level = dotcnt / 2;
		fa[dotcnt / 2].push_back(i);
		tags[i].fa = fa[dotcnt / 2-1 ].back();
		int pos = str.find('#');
		if (pos > 0)
		{
			tags[i].name = str.substr(dotcnt, pos - dotcnt-1);
			tags[i].id = str.substr(pos);
		}
		else
		{
			transform(str.begin(), str.end(), str.begin(), ::tolower);
			tags[i].name = str.substr(dotcnt);
		}
	}
	for (int i = 0; i < m; i++)
	{
		getline(cin, str);
		int pos = str.find(' ');
		if (pos < 0)
		{
			if (str[0] != '#')
			{
				transform(str.begin(), str.end(), str.begin(), ::tolower);
				int cnt = 0;
				queue<int> tmp;
				for (int j = 0; j < n; j++)
				{
					if (tags[j].name == str)
					{
						cnt++;
						tmp.push(j+1);
					}
				}
				cout << cnt;
				while (!tmp.empty())
				{
					cout << " " << tmp.front();
					tmp.pop();
				}
				cout << endl;
			}
			else
			{
				int cnt = 0;
				queue<int> tmp;
				for (int j = 0; j < n; j++)
				{
					if (tags[j].id == str)
					{
						cnt++;
						tmp.push(j + 1);
					}
				}
				cout << cnt;
				while (!tmp.empty())
				{
					cout << " " << tmp.front();
					tmp.pop();
				}
				cout << endl;
			}
		}
		else
		{

			vector<string> vis;
			int pos,len=0;
			int cnt = 0;
			queue<int> ans;
			while ((pos = str.find(' ')) > 0)
			{
				string t;
				t = str.substr(0, pos);
				if(t[0]!='#') transform(t.begin(), t.end(), t.begin(), ::tolower);
				len++;
				vis.push_back(t);
				str = str.substr(pos + 1);
				if(str[0]!='#') transform(str.begin(), str.end(), str.begin(), ::tolower);
			}
			for (int j = 0; j < n; j++)
			{
				int tmplen = len;
				if(tags[j].name==str||tags[j].id==str)
				{
					for (int k = j - 1; k >= 0 && tags[k].level <= tags[j].level; k--)
					{
						if (tags[k].level < tags[j].level)
							if(tags[k].id==vis[tmplen-1]||tags[k].name==vis[tmplen-1])
							{
								tmplen--;
								if (!tmplen) break;
							}
					}
				}
				if (!tmplen)
				{
					ans.push(j + 1);
					cnt++;
				}
			}
			cout << cnt;
			while (!ans.empty())
			{
				cout << " " << ans.front();
				ans.pop();
			}
			cout << endl;
		}
	}
	return 0;
}